The Angular Size of the Smallest Features That a Telescope Can See Is Called the Angular ________.

Telescope for observations with visible light

An optical telescope is a telescope that gathers and focuses light mainly from the visible role of the electromagnetic spectrum, to create a magnified image for direct visual inspection, to make a photograph, or to collect information through electronic epitome sensors.

There are three principal types of optical telescope:

• Refracting telescopes, which apply lenses and less commonly also prisms (dioptrics)
• Reflecting telescopes, which employ mirrors (catoptrics)
• Catadioptric telescopes, which combine lenses and mirrors

An optical telescope's ability to resolve small-scale details is directly related to the diameter (or aperture) of its objective (the primary lens or mirror that collects and focuses the light), and its calorie-free-gathering ability is related to the area of the objective. The larger the objective, the more calorie-free the telescope collects and the finer item it resolves.

People use optical telescopes (including monoculars and binoculars) for outdoor activities such every bit observational astronomy, ornithology, pilotage, hunting and reconnaissance, besides as indoor/semi-outdoor activities such as watching performance arts and spectator sports.

History [edit]

The telescope is more than a discovery of optical craftsmen than an invention of a scientist.^{[1] [two]} The lens and the properties of refracting and reflecting light had been known since antiquity, and theory on how they worked was developed past ancient Greek philosophers, preserved and expanded on in the medieval Islamic world, and had reached a significantly advanced state by the fourth dimension of the telescope's invention in early on modern Europe.^{[3] [4]} But the most significant step cited in the invention of the telescope was the evolution of lens manufacture for spectacles,^{[2] [5] [6]} outset in Venice and Florence in the thirteenth century,^[7] and afterwards in the spectacle making centers in both the Netherlands and Federal republic of germany.^[eight] Information technology is in the netherlands in 1608 where the first documents describing a refracting optical telescope surfaced in the form of a patent filed by spectacle maker Hans Lippershey, followed a few weeks later by claims by Jacob Metius, and a 3rd unknown applicant, that they besides knew of this "art".^[9]

Word of the invention spread fast and Galileo Galilei, on hearing of the device, was making his own improved designs inside a year and was the kickoff to publish astronomical results using a telescope.^[10] Galileo's telescope used a convex objective lens and a concave eye lens, a pattern is now chosen a Galilean telescope. Johannes Kepler proposed an comeback on the blueprint^[xi] that used a convex eyepiece, often called the Keplerian Telescope.

The side by side big step in the development of refractors was the advent of the Achromatic lens in the early 18th century,^[12] which corrected the chromatic abnormality in Keplerian telescopes upwards to that time—allowing for much shorter instruments with much larger objectives.^{[ citation needed ]}

For reflecting telescopes, which use a curved mirror in place of the objective lens, theory preceded practice. The theoretical basis for curved mirrors behaving similar to lenses was probably established by Alhazen, whose theories had been widely disseminated in Latin translations of his piece of work.^[13] Soon later on the invention of the refracting telescope, Galileo, Giovanni Francesco Sagredo, and others, spurred on by their knowledge that curved mirrors had similar properties to lenses, discussed the idea of building a telescope using a mirror as the paradigm forming objective.^[fourteen] The potential advantages of using parabolic mirrors (primarily a reduction of spherical aberration with emptying of chromatic aberration) led to several proposed designs for reflecting telescopes,^[15] the well-nigh notable of which was published in 1663 by James Gregory and came to exist called the Gregorian telescope,^{[16] [17]} but no working models were built. Isaac Newton has been generally credited with constructing the get-go practical reflecting telescopes, the Newtonian telescope, in 1668^[18] although due to their difficulty of structure and the poor performance of the speculum metal mirrors used it took over 100 years for reflectors to become popular. Many of the advances in reflecting telescopes included the perfection of parabolic mirror fabrication in the 18th century,^[nineteen] argent coated glass mirrors in the 19th century, long-lasting aluminum coatings in the 20th century,^[xx] segmented mirrors to permit larger diameters, and active optics to compensate for gravitational deformation. A mid-20th century innovation was catadioptric telescopes such every bit the Schmidt camera, which uses both a lens (corrector plate) and mirror equally primary optical elements, mainly used for broad field imaging without spherical aberration.^{[ citation needed ]}

The late 20th century has seen the development of adaptive eyes and space telescopes to overcome the problems of astronomical seeing.^{[ commendation needed ]}

The electronics revolution of the early 21st century led to the development of computer-continued telescopes in the 2010s that allow not-professional person skywatchers to observe stars and satellites using relatively low-toll equipment past taking advantage of digital astrophotographic techniques developed by professional astronomers over previous decades. An electronic connection to a reckoner (smartphone, pad, or laptop) is required to brand astronomical observations from the telescopes. The digital technology allows multiple images to be stacked while subtracting the dissonance component of the ascertainment producing images of Messier objects and faint stars as dim as an credible magnitude of fifteen with consumer-class equipment.^{[21] [22]}

Principles [edit]

The basic scheme is that the main light-gathering element, the objective (1) (the convex lens or concave mirror used to assemble the incoming light), focuses that calorie-free from the distant object (four) to a focal plane where information technology forms a real prototype (5). This epitome may be recorded or viewed through an eyepiece (2), which acts like a magnifying glass. The eye (3) then sees an inverted, magnified virtual image (6) of the object.

Schematic of a Keplerian refracting telescope. The arrow at (4) is a (notional) representation of the original image; the pointer at (5) is the inverted image at the focal plane; the arrow at (6) is the virtual image that forms in the viewer'south visual sphere. The red rays produce the midpoint of the arrow; two other sets of rays (each black) produce its head and tail.

Inverted images [edit]

Most telescope designs produce an inverted image at the focal aeroplane; these are referred to as inverting telescopes. In fact, the epitome is both turned upside down and reversed left to correct, so that birthday it is rotated by 180 degrees from the object orientation. In astronomical telescopes the rotated view is normally non corrected, since it does not bear upon how the telescope is used. Nonetheless, a mirror diagonal is frequently used to place the eyepiece in a more convenient viewing location, and in that example the image is erect, only still reversed left to right. In terrestrial telescopes such as spotting scopes, monoculars and binoculars, prisms (e.g., Porro prisms) or a relay lens between objective and eyepiece are used to correct the image orientation. There are telescope designs that do non present an inverted image such equally the Galilean refractor and the Gregorian reflector. These are referred to as erecting telescopes.

Design variants [edit]

Many types of telescope fold or divert the optical path with secondary or tertiary mirrors. These may be integral office of the optical design (Newtonian telescope, Cassegrain reflector or similar types), or may simply be used to place the eyepiece or detector at a more convenient position. Telescope designs may also use specially designed additional lenses or mirrors to meliorate image quality over a larger field of view.

Characteristics [edit]

Blueprint specifications relate to the characteristics of the telescope and how it performs optically. Several properties of the specifications may change with the equipment or accessories used with the telescope; such equally Barlow lenses, star diagonals and eyepieces. These interchangeable accessories don't alter the specifications of the telescope, nonetheless they alter the way the telescope's backdrop function, typically magnification, apparent field of view (FOV) and actual field of view.

Surface resolvability [edit]

The smallest resolvable surface area of an object, every bit seen through an optical telescope, is the limited physical expanse that can be resolved. It is analogous to angular resolution, but differs in definition: instead of separation ability between bespeak-low-cal sources it refers to the physical area that tin be resolved. A familiar manner to express the characteristic is the resolvable power of features such every bit Moon craters or Sun spots. Expression using the formula is given by twice the resolving ability ${\displaystyle R}$ over aperture diameter ${\displaystyle D}$ multiplied by the objects diameter ${\displaystyle D_{ob}}$ multiplied by the constant ${\displaystyle \Phi }$ all divided by the objects apparent diameter ${\displaystyle D_{a}}$ .^{[23] [24]}

Resolving power ${\displaystyle R}$ is derived from the wavelength ${\displaystyle {\lambda }}$ using the same unit of measurement as discontinuity; where 550 nm to mm is given by: ${\displaystyle R={\frac {\lambda }{10^{six}}}={\frac {550}{10^{6}}}=0.00055}$ .
The constant ${\displaystyle \Phi }$ is derived from radians to the same unit equally the object's apparent diameter; where the Moon's credible diameter of ${\displaystyle D_{a}={\frac {313\Pi }{10800}}}$ radians to arcsecs is given past: ${\displaystyle D_{a}={\frac {313\Pi }{10800}}\cdot 206265=1878}$ .

An instance using a telescope with an aperture of 130 mm observing the Moon in a 550 nm wavelength, is given past: ${\displaystyle F={\frac {{\frac {2R}{D}}\cdot D_{ob}\cdot \Phi }{D_{a}}}={\frac {{\frac {2\cdot 0.00055}{130}}\cdot 3474.2\cdot 206265}{1878}}\approx iii.22}$

The unit used in the object diameter results in the smallest resolvable features at that unit. In the above example they are approximated in kilometers resulting in the smallest resolvable Moon craters existence three.22 km in diameter. The Hubble Space Telescope has a principal mirror discontinuity of 2400 mm that provides a surface resolvability of Moon craters beingness 174.9 meters in diameter, or sunspots of 7365.2 km in bore.

Athwart resolution [edit]

Ignoring blurring of the prototype by turbulence in the temper (atmospheric seeing) and optical imperfections of the telescope, the athwart resolution of an optical telescope is determined by the diameter of the master mirror or lens gathering the light (too termed its "aperture").

The Rayleigh criterion for the resolution limit ${\displaystyle \alpha _{R}}$ (in radians) is given by

${\displaystyle \sin(\alpha _{R})=1.22{\frac {\lambda }{D}}}$

where ${\displaystyle \lambda }$ is the wavelength and ${\displaystyle D}$ is the aperture. For visible lite ( ${\displaystyle \lambda }$ = 550 nm) in the small-bending approximation, this equation can be rewritten:

${\displaystyle \alpha _{R}={\frac {138}{D}}}$

Here, ${\displaystyle \alpha _{R}}$ denotes the resolution limit in arcseconds and ${\displaystyle D}$ is in millimeters. In the ideal case, the two components of a double star system tin exist discerned even if separated by slightly less than ${\displaystyle \alpha _{R}}$ . This is taken into business relationship past the Dawes limit

${\displaystyle \alpha _{D}={\frac {116}{D}}}$

The equation shows that, all else being equal, the larger the discontinuity, the better the athwart resolution. The resolution is not given by the maximum magnification (or "power") of a telescope. Telescopes marketed by giving high values of the maximum ability oftentimes deliver poor images.

For large ground-based telescopes, the resolution is limited by atmospheric seeing. This limit can be overcome past placing the telescopes higher up the atmosphere, e.1000., on the summits of high mountains, on balloons and high-flying airplanes, or in space. Resolution limits can also be overcome past adaptive eyes, speckle imaging or lucky imaging for basis-based telescopes.

Recently, it has become practical to perform aperture synthesis with arrays of optical telescopes. Very high resolution images tin exist obtained with groups of widely spaced smaller telescopes, linked together past advisedly controlled optical paths, simply these interferometers tin merely be used for imaging bright objects such every bit stars or measuring the brilliant cores of agile galaxies.

Focal length and focal ratio [edit]

The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical organisation in air, it is the distance over which initially collimated rays are brought to a focus. A system with a shorter focal length has greater optical power than one with a long focal length; that is, it bends the rays more strongly, bringing them to a focus in a shorter distance. In astronomy, the f-number is commonly referred to equally the focal ratio notated equally ${\displaystyle N}$ . The focal ratio of a telescope is defined as the focal length ${\displaystyle f}$ of an objective divided by its diameter ${\displaystyle D}$ or by the diameter of an aperture stop in the system. The focal length controls the field of view of the instrument and the scale of the paradigm that is presented at the focal plane to an eyepiece, film plate, or CCD.

An example of a telescope with a focal length of 1200 mm and discontinuity bore of 254 mm is given by: ${\displaystyle N={\frac {f}{D}}={\frac {1200}{254}}\approx iv.7}$

Numerically large Focal ratios are said to be long or irksome. Small numbers are brusque or fast. There are no sharp lines for determining when to use these terms, and an individual may consider their own standards of determination. Amid contemporary astronomical telescopes, any telescope with a focal ratio slower (bigger number) than f/12 is generally considered dull, and any telescope with a focal ratio faster (smaller number) than f/6, is considered fast. Faster systems often have more optical aberrations away from the centre of the field of view and are generally more demanding of eyepiece designs than slower ones. A fast system is often desired for applied purposes in astrophotography with the purpose of gathering more photons in a given time menstruum than a slower system, assuasive time lapsed photography to process the result faster.

Wide-field telescopes (such every bit astrographs), are used to rail satellites and asteroids, for cosmic-ray inquiry, and for astronomical surveys of the sky. Information technology is more difficult to reduce optical aberrations in telescopes with low f-ratio than in telescopes with larger f-ratio.

Low-cal-gathering power [edit]

The Keck Ii telescope gathers light by using 36 segmented hexagonal mirrors to create a 10 chiliad (33 ft) aperture primary mirror

The light-gathering power of an optical telescope, also referred to as light grasp or discontinuity gain, is the power of a telescope to collect a lot more light than the human centre. Its light-gathering ability is probably its most important feature. The telescope acts as a light bucket, collecting all of the photons that come downwardly on it from a far away object, where a larger bucket catches more photons resulting in more received light in a given time flow, effectively brightening the image. This is why the pupils of your eyes enlarge at dark so that more than low-cal reaches the retinas. The gathering power ${\displaystyle P}$ compared against a homo centre is the squared issue of the division of the aperture ${\displaystyle D}$ over the observer'due south pupil diameter ${\displaystyle D_{p}}$ ,^{[23] [24]} with an average adult having a pupil diameter of 7 mm. Younger persons host larger diameters, typically said to be ix mm, every bit the diameter of the educatee decreases with age.

An example gathering power of an aperture with 254 mm compared to an adult pupil bore existence 7 mm is given by: ${\displaystyle P=\left({\frac {D}{D_{p}}}\right)^{2}=\left({\frac {254}{seven}}\right)^{2}\approx 1316.seven}$

Light-gathering power can be compared betwixt telescopes by comparing the areas ${\displaystyle A}$ of the two different apertures.

As an example, the light-gathering power of a 10-meter telescope is 25x that of a ii-meter telescope: ${\displaystyle p={\frac {A_{ane}}{A_{two}}}={\frac {\pi five^{2}}{\pi i^{2}}}=25}$

For a survey of a given area, the field of view is only equally of import as raw light gathering power. Survey telescopes such equally the Big Synoptic Survey Telescope try to maximize the product of mirror surface area and field of view (or etendue) rather than raw low-cal gathering ability lone.

Magnification [edit]

The magnification through a telescope makes an object announced larger while limiting the FOV. Magnification is often misleading equally the optical power of the telescope, its feature is the most misunderstood term used to describe the observable world.^{[ clarification needed ]} At higher magnifications the image quality significantly reduces, usage of a Barlow lens increases the constructive focal length of an optical organization—multiplies prototype quality reduction.

Similar minor effects may be present when using star diagonals, every bit low-cal travels through a multitude of lenses that increment or decrease effective focal length. The quality of the image generally depends on the quality of the optics (lenses) and viewing atmospheric condition—not on magnification.

Magnification itself is limited by optical characteristics. With whatever telescope or microscope, beyond a practical maximum magnification, the image looks bigger merely shows no more detail. Information technology occurs when the finest detail the instrument can resolve is magnified to match the finest detail the eye can see. Magnification beyond this maximum is sometimes called empty magnification.

To get the most item out of a telescope, information technology is critical to choose the right magnification for the object being observed. Some objects appear best at low ability, some at high power, and many at a moderate magnification. There are two values for magnification, a minimum and maximum. A wider field of view eyepiece may exist used to keep the same eyepiece focal length whilst providing the same magnification through the telescope. For a good quality telescope operating in good atmospheric weather condition, the maximum usable magnification is express past diffraction.

Visual [edit]

The visual magnification ${\displaystyle M}$ of the field of view through a telescope can be determined by the telescope'southward focal length ${\displaystyle f}$ divided by the eyepiece focal length ${\displaystyle f_{due east}}$ (or diameter).^{[23] [24]} The maximum is limited by the focal length of the eyepiece.

An case of visual magnification using a telescope with a 1200 mm focal length and 3 mm eyepiece is given past: ${\displaystyle M={\frac {f}{f_{due east}}}={\frac {1200}{iii}}=400}$

Minimum [edit]

There is a lowest usable magnification on a telescope. The increase in brightness with reduced magnification has a limit related to something called the go out pupil. The go out educatee is the cylinder of light coming out of the eyepiece, hence the lower the magnification, the larger the exit pupil. The minimum ${\displaystyle M_{yard}}$ tin can be calculated by dividing the telescope discontinuity ${\displaystyle D}$ over the exit student diameter ${\displaystyle D_{ep}}$ .^[25] Decreasing the magnification past this limit cannot increase effulgence, at this limit there is no benefit for decreased magnification. Also calculating the exit pupil ${\displaystyle D_{ep}}$ is a sectionalization of the aperture diameter ${\displaystyle D}$ and the visual magnification ${\displaystyle M}$ used. The minimum often may not be reachable with some telescopes, a telescope with a very long focal length may crave a longer-focal-length eyepiece than is possible.

An example of the lowest usable magnification using a 254 mm aperture and vii mm get out pupil is given by: ${\displaystyle M_{one thousand}={\frac {D}{D_{ep}}}={\frac {254}{7}}\approx 36}$ , whilst the get out educatee diameter using a 254 mm aperture and 36x magnification is given by: ${\displaystyle D_{ep}={\frac {D}{M}}={\frac {254}{36}}\approx seven}$

Optimum [edit]

A useful reference is:

• For small objects with low surface brightness (such as galaxies), use a moderate magnification.
• For small objects with loftier surface brightness (such as planetary nebulae), utilise a loftier magnification.
• For large objects regardless of surface effulgence (such as lengthened nebulae), use low magnification, often in the range of minimum magnification.

Simply personal experience determines the best optimum magnifications for objects, relying on observational skills and seeing weather condition.

Field of view [edit]

Field of view is the extent of the observable earth seen at whatsoever given moment, through an instrument (e.g., telescope or binoculars), or past naked middle. There are diverse expressions of field of view, beingness a specification of an eyepiece or a characteristic determined from an eyepiece and telescope combination. A concrete limit derives from the combination where the FOV cannot be viewed larger than a defined maximum, due to diffraction of the optics.

Apparent [edit]

Apparent field of view (usually referred to as AFOV) is the perceived angular size of the field stop of the eyepiece, typically measured in degrees. It is a fixed property of the eyepiece'south optical design, with common commercially bachelor eyepieces offering a range of credible fields from 40° to 120°. The credible field of view of an eyepiece is express by a combination of the eyepiece's field terminate bore, and focal length, and is contained of magnification used.

In an eyepiece with a very wide credible field of view, the observer may perceive that the view through the telescope stretches out to their peripheral vision, giving a sensation that they are no longer looking through an eyepiece, or that they are closer to the subject of interest than they really are. In contrast, an eyepiece with a narrow apparent field of view may give the sensation of looking through a tunnel or small porthole window, with the black field terminate of the eyepiece occupying most of the observer'south vision.

A wider apparent field of view permits the observer to run into more than of the subject of interest (that is, a wider true field of view) without reducing magnification to do so. Even so, it should be noted the relationship between true field of view, apparent field of view, and magnification is not directly, due to increasing distortion characteristics that correlate with wider credible fields of view. Instead, both true field of view and apparent field of view are consequences of the eyepiece's field stop bore.

Apparent field of view differs from true field of view in and so far as true field of view varies with magnification, whereas apparent field of view does non. The wider field stop of a wide bending eyepiece permits the viewing of a wider section of the real prototype formed at the telescope'southward focal airplane, thus impacting the calculated truthful field of view.

An eyepiece's apparent field of view can influence full view brightness equally perceived by the middle, since the apparent angular size of the field terminate volition determine how much of the observer'southward retina is illuminated by the exit student formed past the eyepiece. However, credible field of view has no touch on the apparent surface brightness (that is, brightness per unit of measurement area) of objects contained within the field of view.

True [edit]

True FOV is the width of what is actually seen through any given eyepiece / telescope combination.

At that place are two formulae for calculating true field of view:

1. Apparent field of view method given by ${\displaystyle v_{t}={\frac {v_{a}}{One thousand}}}$ , where ${\displaystyle v_{t}}$ is the truthful FOV, ${\displaystyle v_{a}}$ is the apparent field of view of the eyepiece, and ${\displaystyle M}$ is the magnification being used. ^{[26] [27]}
2. Eyepiece field stop method given by ${\displaystyle v_{t}={\frac {d_{f}}{f_{t}}}\times 57.three}$ , where ${\displaystyle v_{t}}$ is the truthful FOV, ${\displaystyle d_{f}}$ is the eyepiece field stop diameter in millimeters and ${\displaystyle f_{t}}$ is the focal length of the telescope in millimeters.^{[26] [27]}

The eyepiece field stop method is more accurate than the credible field of view method,^[27] however not all eyepieces accept an easily knowable field stop bore.

Maximum [edit]

Max FOV is the maximum useful true field of view limited by the optics of the telescope. Information technology is a physical limitation where increases beyond the maximum remain at maximum. Max FOV ${\displaystyle v_{1000}}$ is the barrel size ${\displaystyle B}$ over the telescope'due south focal length ${\displaystyle f}$ converted from radian to degrees.^{[23] [24]}

An example of max FOV using a telescope with a butt size of 31.75 mm (1.25 inches) and focal length of 1200 mm is given by: ${\displaystyle v_{m}=B\cdot {\frac {\frac {180}{\pi }}{f}}\approx 31.75\cdot {\frac {57.2958}{1200}}\approx ane.52^{\circ }}$

Observing through a telescope [edit]

There are many properties of optical telescopes and the complexity of observation using one can be a daunting task; feel and experimentation are the major contributors to understanding how to maximize 1'due south observations. In practice, only two master properties of a telescope make up one's mind how ascertainment differs: the focal length and aperture. These relate equally to how the optical arrangement views an object or range and how much light is gathered through an ocular eyepiece. Eyepieces farther determine how the field of view and magnification of the observable world modify.

Observable world [edit]

The appreciable earth is what can be seen using a telescope. When viewing an object or range, the observer may utilise many different techniques. Understanding what tin be viewed and how to view information technology depends on the field of view. Viewing an object at a size that fits entirely in the field of view is measured using the two telescope properties—focal length and discontinuity, with the inclusion of an ocular eyepiece with suitable focal length (or diameter). Comparison the observable world and the angular diameter of an object shows how much of the object we come across. However, the relationship with the optical system may not result in loftier surface effulgence. Celestial objects are often dim considering of their vast altitude, and particular may be express by diffraction or unsuitable optical backdrop.

Field of view and magnification human relationship [edit]

Finding what can be seen through the optical system begins with the eyepiece providing the field of view and magnification; the magnification is given by the partition of the telescope and eyepiece focal lengths. Using an example of an amateur telescope such as a Newtonian telescope with an aperture ${\displaystyle D}$ of 130 mm (5") and focal length ${\displaystyle f}$ of 650 mm (25.5 inches), one uses an eyepiece with a focal length ${\displaystyle d}$ of 8 mm and credible FOV ${\displaystyle v_{a}}$ of 52°. The magnification at which the observable world is viewed is given by: ${\displaystyle M={\frac {f}{d}}={\frac {650}{8}}=81.25}$ . The field of view ${\displaystyle v_{t}}$ requires the magnification, which is formulated by its division over the apparent field of view: ${\displaystyle v_{t}={\frac {v_{a}}{M}}={\frac {52}{81.25}}=0.64}$ . The resulting true field of view is 0.64°, non allowing an object such as the Orion nebula, which appears elliptical with an angular diameter of 65 × threescore arcminutes, to be viewable through the telescope in its entirety, where the whole of the nebula is inside the observable earth. Using methods such as this tin can greatly increase 1'southward viewing potential ensuring the appreciable world can contain the entire object, or whether to increment or decrease magnification viewing the object in a different aspect.

Brightness factor [edit]

The surface brightness at such a magnification significantly reduces, resulting in a far dimmer appearance. A dimmer appearance results in less visual detail of the object. Details such as thing, rings, spiral arms, and gases may be completely subconscious from the observer, giving a far less consummate view of the object or range. Physics dictates that at the theoretical minimum magnification of the telescope, the surface brightness is at 100%. Practically, however, various factors prevent 100% brightness; these include telescope limitations (focal length, eyepiece focal length, etc.) and the historic period of the observer.

Age plays a part in brightness, equally a contributing factor is the observer's pupil. With age the pupil naturally shrinks in diameter; generally accustomed a young adult may have a seven mm bore pupil, an older developed as trivial as 5 mm, and a younger person larger at nine mm. The minimum magnification ${\displaystyle m}$ can be expressed as the sectionalization of the aperture ${\displaystyle D}$ and pupil ${\displaystyle p}$ diameter given by: ${\displaystyle g={\frac {D}{d}}={\frac {130}{seven}}\approx 18.six}$ . A problematic instance may be apparent, achieving a theoretical surface brightness of 100%, as the required effective focal length of the optical arrangement may require an eyepiece with too big a diameter.

Some telescopes cannot reach the theoretical surface brightness of 100%, while some telescopes can achieve it using a very pocket-sized-diameter eyepiece. To find what eyepiece is required to go minimum magnification one tin rearrange the magnification formula, where it is now the division of the telescope's focal length over the minimum magnification: ${\displaystyle {\frac {F}{k}}={\frac {650}{18.vi}}\approx 35}$ . An eyepiece of 35 mm is a non-standard size and would not be purchasable; in this scenario to achieve 100% 1 would require a standard manufactured eyepiece size of 40 mm. Equally the eyepiece has a larger focal length than the minimum magnification, an affluence of wasted light is not received through the optics.

Exit educatee [edit]

The limit to the increase in surface effulgence every bit i reduces magnification is the exit student: a cylinder of light that projects out the eyepiece to the observer. An exit pupil must match or exist smaller in diameter than ane's educatee to receive the total corporeality of projected light; a larger exit student results in the wasted calorie-free. The exit pupil ${\displaystyle e}$ can be derived with from division of the telescope aperture ${\displaystyle D}$ and the minimum magnification ${\displaystyle m}$ , derived by: ${\displaystyle east={\frac {D}{1000}}={\frac {130}{xviii.vi}}\approx vii}$ . The pupil and go out pupil are almost identical in diameter, giving no wasted observable light with the optical arrangement. A vii mm educatee falls slightly brusque of 100% brightness, where the surface brightness ${\displaystyle B}$ can be measured from the production of the constant 2, by the foursquare of the pupil ${\displaystyle p}$ resulting in: ${\displaystyle B=ii*p^{2}=two*7^{2}=98}$ . The limitation here is the pupil diameter; it's an unfortunate result and degrades with age. Some observable light loss is expected and decreasing the magnification cannot increase surface effulgence in one case the system has reached its minimum usable magnification, hence why the term is referred to as usable.

These eyes represent a scaled figure of the human eye where fifteen px = 1 mm, they have a pupil diameter of 7 mm. Effigy A has an get out pupil diameter of xiv mm, which for astronomy purposes results in a 75% loss of low-cal. Figure B has an exit pupil of 6.4 mm, which allows the full 100% of observable light to be perceived by the observer.

Image Calibration [edit]

When using a CCD to tape observations, the CCD is placed in the focal plane. Image scale (sometimes called plate scale) is how the athwart size of the object existence observed is related to the physical size of the projected image in the focal plane

${\displaystyle i={\frac {\alpha }{s}},}$

where ${\displaystyle i}$ is the prototype scale, ${\displaystyle \alpha }$ is the angular size of the observed object, and ${\displaystyle south}$ is the physical size of the projected prototype. In terms of focal length prototype scale is

${\displaystyle i={\frac {1}{f}},}$

where ${\displaystyle i}$ is measured in radians per meter (rad/m), and ${\displaystyle f}$ is measured in meters. Normally ${\displaystyle i}$ is given in units of arcseconds per millimeter ("/mm). So if the focal length is measured in millimeters, the prototype scale is

${\displaystyle i\ (''/\mathrm {mm} )={\frac {1}{f\ (\mathrm {mm} )}}\left[{\frac {180\times 3600}{\pi }}\right].}$

The derivation of this equation is fairly straightforward and the issue is the same for reflecting or refracting telescopes. However, conceptually it is easier to derive by because a reflecting telescope. If an extended object with angular size ${\displaystyle \blastoff }$ is observed through a telescope, then due to the Laws of reflection and Trigonometry the size of the paradigm projected onto the focal plane will be

${\displaystyle southward=\tan(\alpha )f.}$

Thefore, the paradigm scale (angular size of object divided by size of projected epitome) will exist

${\displaystyle i={\frac {\blastoff }{due south}}={\frac {\alpha }{\tan(\blastoff )f}},}$

and by using the pocket-size angle relation ${\displaystyle \tan(a)\approx a}$ , when ${\displaystyle a\ll 1}$ (N.B. merely valid if ${\displaystyle a}$ is in radians), we obtain

${\displaystyle i={\frac {\alpha }{\alpha f}}={\frac {ane}{f}}.}$

Imperfect images [edit]

No telescope can form a perfect image. Fifty-fifty if a reflecting telescope could accept a perfect mirror, or a refracting telescope could have a perfect lens, the effects of aperture diffraction are unavoidable. In reality, perfect mirrors and perfect lenses practice not be, so image aberrations in add-on to aperture diffraction must be taken into account. Paradigm aberrations tin can exist broken down into two chief classes, monochromatic, and polychromatic. In 1857, Philipp Ludwig von Seidel (1821–1896) decomposed the start society monochromatic aberrations into five constituent aberrations. They are now commonly referred to every bit the five Seidel Aberrations.

The 5 Seidel aberrations [edit]

Spherical abnormality

The difference in focal length between paraxial rays and marginal rays, proportional to the square of the objective diameter.

Coma

A defect by which points appear equally comet-like asymmetrical patches of lite with tails, which makes measurement very imprecise. Its magnitude is usually deduced from the optical sine theorem.

Astigmatism

The prototype of a point forms focal lines at the sagittal and tangental foci and in betwixt (in the absence of coma) an elliptical shape.

Curvature of Field

The Petzval field curvature ways that the image, instead of lying in a aeroplane, actually lies on a curved surface, described equally hollow or circular. This causes bug when a flat imaging device is used e.g., a photographic plate or CCD epitome sensor.

Distortion

Either barrel or pincushion, a radial baloney that must be corrected when combining multiple images (similar to stitching multiple photos into a panoramic photo).

Optical defects are always listed in the above order, since this expresses their interdependence as first order aberrations via moves of the exit/entrance pupils. The first Seidel aberration, Spherical Abnormality, is independent of the position of the exit pupil (every bit information technology is the same for axial and extra-axial pencils). The second, blackout, changes as a function of pupil distance and spherical abnormality, hence the well-known result that it is incommunicable to correct the coma in a lens gratis of spherical abnormality by simply moving the student. Like dependencies affect the remaining aberrations in the listing.

Chromatic aberrations [edit]

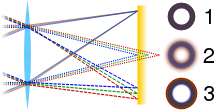
Comparison of an ideal prototype of a ring (1) and ones with only centric (2) and only transverse (three) chromatic abnormality

Longitudinal chromatic aberration: As with spherical aberration this is the same for axial and oblique pencils.

Transverse chromatic aberration (chromatic aberration of magnification)

Astronomical research telescopes [edit]

Ii of the four Unit of measurement Telescopes that brand upward the ESO's VLT, on a remote mountaintop, 2600 metres above sea level in the Chilean Atacama Desert.

Optical telescopes have been used in astronomical research since the time of their invention in the early on 17th century. Many types take been constructed over the years depending on the optical technology, such every bit refracting and reflecting, the nature of the calorie-free or object being imaged, and fifty-fifty where they are placed, such as space telescopes. Some are classified past the task they perform such as Solar telescopes.

Large reflectors [edit]

Nigh all large research-grade astronomical telescopes are reflectors. Some reasons are:

• In a lens the unabridged book of material has to be gratis of imperfection and inhomogeneities, whereas in a mirror, only one surface has to be perfectly polished.
• Light of different colors travels through a medium other than vacuum at different speeds. This causes chromatic aberration.
• Reflectors piece of work in a wider spectrum of light since certain wavelengths are absorbed when passing through drinking glass elements similar those found in a refractor or catadioptric.
• There are technical difficulties involved in manufacturing and manipulating big-bore lenses. One of them is that all real materials sag in gravity. A lens can merely exist held by its perimeter. A mirror, on the other hand, can be supported past the whole side opposite to its reflecting face.

Comparison of nominal sizes of primary mirrors of some notable optical telescopes

Near big research reflectors operate at unlike focal planes, depending on the type and size of the instrument being used. These including the prime focus of the principal mirror, the cassegrain focus (light bounced back down behind the main mirror), and even external to the telescope all together (such as the Nasmyth and coudé focus).^[28]

A new era of telescope making was inaugurated by the Multiple Mirror Telescope (MMT), with a mirror composed of six segments synthesizing a mirror of iv.5 meters diameter. This has now been replaced by a single 6.5 m mirror. Its example was followed past the Keck telescopes with 10 m segmented mirrors.

The largest current ground-based telescopes have a primary mirror of betwixt six and 11 meters in diameter. In this generation of telescopes, the mirror is commonly very thin, and is kept in an optimal shape by an assortment of actuators (see active optics). This applied science has driven new designs for hereafter telescopes with diameters of 30, 50 and fifty-fifty 100 meters.

Relatively inexpensive, mass-produced ~2 meter telescopes have recently been developed and take made a significant impact on astronomy enquiry. These allow many astronomical targets to be monitored continuously, and for large areas of sky to be surveyed. Many are robotic telescopes, computer controlled over the internet (run across east.yard. the Liverpool Telescope and the Faulkes Telescope North and S), assuasive automated follow-up of astronomical events.

Initially the detector used in telescopes was the man eye. Later, the sensitized photographic plate took its place, and the spectrograph was introduced, allowing the gathering of spectral information. After the photographic plate, successive generations of electronic detectors, such equally the charge-coupled device (CCDs), have been perfected, each with more sensitivity and resolution, and often with a wider wavelength coverage.

Current research telescopes have several instruments to choose from such equally:

• imagers, of dissimilar spectral responses
• spectrographs, useful in dissimilar regions of the spectrum
• polarimeters, that detect lite polarization.

The phenomenon of optical diffraction sets a limit to the resolution and epitome quality that a telescope tin can attain, which is the constructive expanse of the Blusterous disc, which limits how close 2 such discs tin exist placed. This absolute limit is called the diffraction limit (and may be approximated by the Rayleigh criterion, Dawes limit or Sparrow's resolution limit). This limit depends on the wavelength of the studied light (so that the limit for ruby-red light comes much earlier than the limit for blue lite) and on the bore of the telescope mirror. This ways that a telescope with a sure mirror diameter can theoretically resolve upwardly to a certain limit at a certain wavelength. For conventional telescopes on Earth, the diffraction limit is not relevant for telescopes bigger than nearly ten cm. Instead, the seeing, or blur caused by the atmosphere, sets the resolution limit. But in space, or if adaptive eyes are used, and so reaching the diffraction limit is sometimes possible. At this indicate, if greater resolution is needed at that wavelength, a wider mirror has to be built or discontinuity synthesis performed using an array of nearby telescopes.

In recent years, a number of technologies to overcome the distortions caused past temper on ground-based telescopes take been developed, with good results. Come across adaptive optics, speckle imaging and optical interferometry.

See likewise [edit]

• Astronomy
• Astrophotography
• Amateur telescope making
• Bahtinov mask
• Binoculars
• Carey mask
• Chinese Future Giant Telescope
• Depth of field
• Dipleidoscope
• World event
• Hartmann mask
• History of optics
• List of optical telescopes
• List of largest optical reflecting telescopes (with mirrors)
• List of largest optical refracting telescopes (with lenses)
• List of largest optical telescopes historically
• List of solar telescopes (for the Sun)
• List of infinite telescopes
• List of telescope types

References [edit]

1. ^ galileo.rice.edu The Galileo Projection > Science > The Telescope by Al Van Helden – "the telescope was not the invention of scientists; rather, it was the production of craftsmen."
2. ^ ^{a b} Fred Watson (2007). Ian Stargazer: The Life and Times of the Telescope. Allen & Unwin. p. 55. ISBN978-1-74176-392-8.
3. ^ Henry C. King (2003). The History of the Telescope. Courier Corporation. pp. 25–29. ISBN978-0-486-43265-vi.
4. ^ progression is followed through Robert Grosseteste Witelo, Roger Bacon, through Johannes Kepler, D. C. Lindberg, Theories of Vision from al-Kindi to Kepler, (Chicago: Univ. of Chicago Pr., 1976), pp. 94–99
5. ^ galileo.rice.edu The Galileo Project > Science > The Telescope by Al Van Helden
6. ^ Renaissance Vision from Spectacles to Telescopes By Vincent Ilardi, page 210
7. ^ galileo.rice.edu The Galileo Project > Scientific discipline > The Telescope by Al Van Helden
8. ^ Henry C. King (2003). The History of the Telescope. Courier Corporation. p. 27. ISBN978-0-486-43265-vi. (spectacles) invention, an important pace in the history of the telescope
9. ^ Albert Van Helden, Sven Dupré, Rob van Gent, The Origins of the Telescope, Amsterdam University Printing, 2010, pages 3-4, xv
10. ^ Albert Van Helden, Sven Dupré, Rob van Gent, The Origins of the Telescope, Amsterdam University Press, 2010, page 183
11. ^ See his books Astronomiae Pars Optica and Dioptrice
12. ^ Sphaera - Peter Dollond answers Jesse Ramsden - A review of the events of the invention of the achromatic doublet with accent on the roles of Hall, Bass, John Dollond and others.
13. ^ Fred Watson (2007). Ian Stargazer: The Life and Times of the Telescope. Allen & Unwin. p. 108. ISBN978-i-74176-392-viii.
14. ^ Fred Watson (2007). Ian Stargazer: The Life and Times of the Telescope. Allen & Unwin. p. 109. ISBN978-one-74176-392-8.
15. ^ works by Bonaventura Cavalieri and Marin Mersenne amongst others take designs for reflecting telescopes
16. ^ Fred Watson (2007). Ian Stargazer: The Life and Times of the Telescope. Allen & Unwin. p. 117. ISBN978-1-74176-392-8.
17. ^ Henry C. Rex (2003). The History of the Telescope. Courier Corporation. p. 71. ISBN978-0-486-43265-half-dozen.
18. ^ A. Rupert Hall (1996). Isaac Newton: Adventurer in Thought . Cambridge University Press. p. 67. ISBN978-0-521-56669-8.
19. ^ Parabolic mirrors were used much earlier, but James Short perfected their construction. See "Reflecting Telescopes (Newtonian Type)". Astronomy Department, University of Michigan.
20. ^ Silvering was introduced by Léon Foucault in 1857, see madehow.com - Inventor Biographies - Jean-Bernard-Léon Foucault Biography (1819–1868), and the adoption of long lasting aluminized coatings on reflector mirrors in 1932. Bakich sample pages Chapter two, Page 3 "John Donavan Stiff, a immature physicist at the California Found of Engineering science, was one of the outset to coat a mirror with aluminum. He did it by thermal vacuum evaporation. The first mirror he aluminized, in 1932, is the earliest known case of a telescope mirror coated by this technique."
21. ^ "Les télescopes connectés débarquent. Episode 2/2 : l'eVscope" [The continued telescopes land. Episode 2/2: the eVscope]. Ciel & espace (in French). Fifty'Association Française d'Astronomie. November 2018. Archived from the original on 29 June 2019. Retrieved 29 June 2019.
22. ^ Billings, Lee (13 September 2018). "New Telescope 'Gives Back the Sky' to Urban center-Dwellers". Scientific American. Archived from the original on 27 March 2019. Retrieved 29 June 2019.
23. ^ ^{a b c d} "Telescope Formulae". SaharaSky Observatory. iii July 2012.
24. ^ ^{a b c d} "Optical Formulae". Ryukyu Astronomy Club. two January 2012.
25. ^ "Telescope Equations". RocketMime. 17 November 2012.
26. ^ ^{a b} "Elementary Formulas for the Telescope Owner". Sky & Telescope. 2017-11-xx. Retrieved 2022-01-28 .
27. ^ ^{a b c} "Make up one's mind Your True Field of View - Astronomy Hacks [Volume]". www.oreilly.com . Retrieved 2022-01-28 .
28. ^ Ian Southward. McLean (2008). Electronic Imaging in Astronomy: Detectors and Instrumentation. Springer Scientific discipline & Business Media. p. 91. ISBN978-3-540-76582-0.

External links [edit]

Media related to Optical telescopes at Wikimedia Commons

• Notes on Apprentice TELESCOPE OPTICS
• Online Telescope Math Calculator
• The Resolution of a Telescope
• skyandtelescope.com – What To Know (about telescopes)

coopersuccall.blogspot.com

Source: https://en.wikipedia.org/wiki/Optical_telescope

Share this post